二進法を勉強したのは、電気の世界で扱う数字が二進法でできているからです。

そこで次に、第三回の講座で数値化した波形が、デジタルの世界で、電気的にどのような形で扱われるかを見てみましょう。いよいよデジタル波形を見て行くわけです。

前回(第三回)の講座で、アナログの波形を下記のような数字列になおしました。

この時私は、「この数字列が、波形がデジタル化された結果というわけです」と解説しましたが、本当はウソでした(^_^;)。実はまだデジタル化されていなかったんですね。数値化はしましたが、十進法で書いてあるからです。二進法にしないと本当のデジタルとは言えません。

そこでこの数字列を二進法に直してみましょう。

12.1. ビット数を決める

十進法を二進法になおすには、まず何ビットあれば表現できるかを決めます。つまり数字が何通り表れるかを考えて、必要なビット数を決めるんです。

では今回の元の波形は、何通りの数字が出てくるんでしたっけ。波形を見てみましょう。

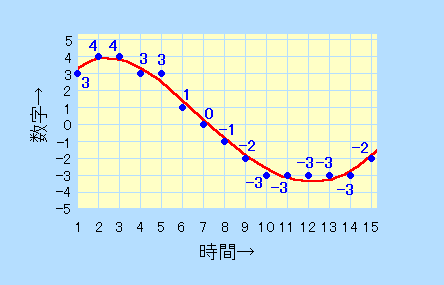
縦軸を見て下さい。メッシュは11とおりですね。この範囲の波形を表現できるようにする、つまり11とおりの数が扱えるようなビット数を、まず選択します。

何ビット必要でしょう。前ページで学習したことを思い出してください。1ビットで2とおり、2ビットで4とおり、3ビットで8とおり、4ビットで16とおりでしたね。

ですから、11とおりの数を表すには、4ビットあればいいわけです。

12.2. マイナスの数が扱えるようにする

それから、いままで扱ってきた表ではマイナスの数が出てきませんでした。そこでマイナスが扱えるような工夫をします。

これは、4ビット＝16とおりの数字の半分をマイナスの数に割り当てることにしましょう。これは、変換表を作り替えるだけで解決します。

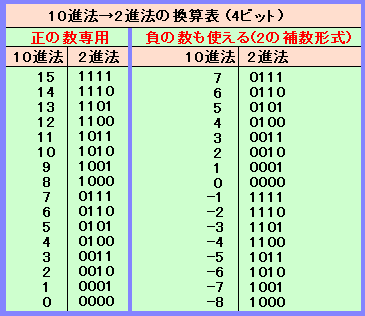
これが作りなおした変換表で、左がいままで見ていた変換、右がマイナス対応の変換です。

まず今までの変換表(正の数だけの変換表)のうち、下半分、つまり十進法で0〜7までの8個はそのままにしておきます。そして、上半分を0の下にくっつけてマイナスの数に割り当てます。いままでの15を-1、14を-2…というようにするわけです。

この形式は非常によく使われるもので「2の補数形式」という形式です。オーディオ波形は必ず正負の数が出てきますので、デジタルオーディオ機器は内部で必ずといってよいほどこの形式を使っています。

なお、使える数は必ず偶数個ですが、一個を0に充てますので、必ずプラス側が一個少なくなります。たとえばCDは16ビットで65536通りの数を使いますが、2の補数で扱いますから、扱える数は−32768〜0〜＋32767となります。ただ、数が十分に多いので、一個ぐらいの差は問題になりません。

12.3. 二進法に置き換えます

さあ、これで変換表が手に入りました。いよいよ置き換えをやります。

まず、先頭の三つくらいやってみましょう。十進法で3、4、4の部分ですね。変換表を見てください。

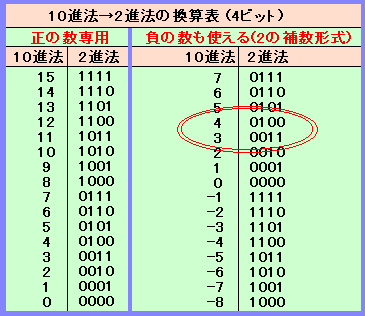
表から3と4は、2進法では0011と0100になります。この調子で、上の数字列を全部二進法の数に直すと、次のようになります。

「…,0011,0100,0100,0011,0011,0001,0000,1111,1110,1101,1101,1101,1101,1101,1110,…」

さあ、これでもともとのアナログ波形を、完全な二進法の数の並んでいるデジタル信号に変換することができました。

(制作/著作 かないまる 2000年8月20日)